|
|
The ability to capture and digitally represent the world continues to evolve. A relatively recent development allows images and videos to capture an entire panorama of 360 degrees horizontally and 180 degrees vertically. These images and videos can be displayed on web pages like this one or virtual reality headsets, allowing people to have an immersive view of the environment and "look around" to see any desired scene angle.
For instance, Figure 1 below initially appears as a standard two-dimensional image; however, after selecting the image by clicking on it, the following keystrokes navigate around the scene:
Alternatively, the following mouse actions alter the point of view:
This blog series explores different representations for storing images, describes how these representations convert from 360-degree coordinates to a flat image representation, different techniques for extracting rectilinear views, and creating optimized code for extracting the views.
Figure 2, below, shows the raw image containing all the pixel data for representing the rectilinear view shown in Figure 1 above.
Multiple file format representations exist for a 360-degree image. The format shown in Figure 2 is referred to as the equirectangular format. The mathematical conversion from the 360-degree view to the equirectangular format makes human understanding of the image challenging. The remainder of this section explains the conversion process for the equirectangular format.
To shoot this scene, a 360-degree camera was placed on a tripod with the edge of a road running directly underneath the camera. This can be seen by changing the Figure 1 view to look directly downward to see the road below. The camera's primary lens faced the fenced yard, with the road extending straight out to the left and right of the camera. Directly behind the camera was the road and then a meadow on the other side of the road.
Further down in this post, additional visualization techniques explain why the road appears to get folded in half.
Two common formats exist for storing 360-degree images: 1) Equirectangular and 2) Cubemap.
The equirectangular format takes a 360-degree image and maps discrete points along the longitude and latitudes to the X and Y locations on the output image. As shown in Figure 3 below, the X coordinates start at -180 degrees and end at 180 degrees in equal parts along the X axis. Likewise, the Y coordinates go from -90 at the bottom of the image to 90 degrees at the top. The equirectangular format always results in a 2:1 ratio image since the horizontal coverage is twice as much as the vertical coverage.
In cases like this blog, the images used are controlled and known to be equirectangular (also known as panorama). In other instances where a person provides a pointer to an image to load, the code must decide whether the image represents a panorama image. One option is to use the 2:1 ratio to "guess" whether the provided image is a panorama. Better yet, the code can examine the metadata within the image file to check if the image has been tagged as a panorama image. https://exiv2.org/tags-xmp-GPano.html defines the eXtensible Metadata Platform (XMP) section (https://www.adobe.com/devnet/xmp.html) of an image that corresponds to images that use the GPano properties. The ProjectionType property defines the storage layout. A value of equirectangular informs software to treat the image as equirectangular.
For instance, the metadata for Figure 2 is:
Figure 4 shows what the data from Figure 3 looks like when the camera is at the center of the sphere and moved around to view different angles within the sphere. As shown, Figure 3 data essentially wraps around the outside of the sphere with the -180 and 180 points meeting directly behind the initial viewing perspective, and the top and bottom of the image converge at the two poles of the sphere.
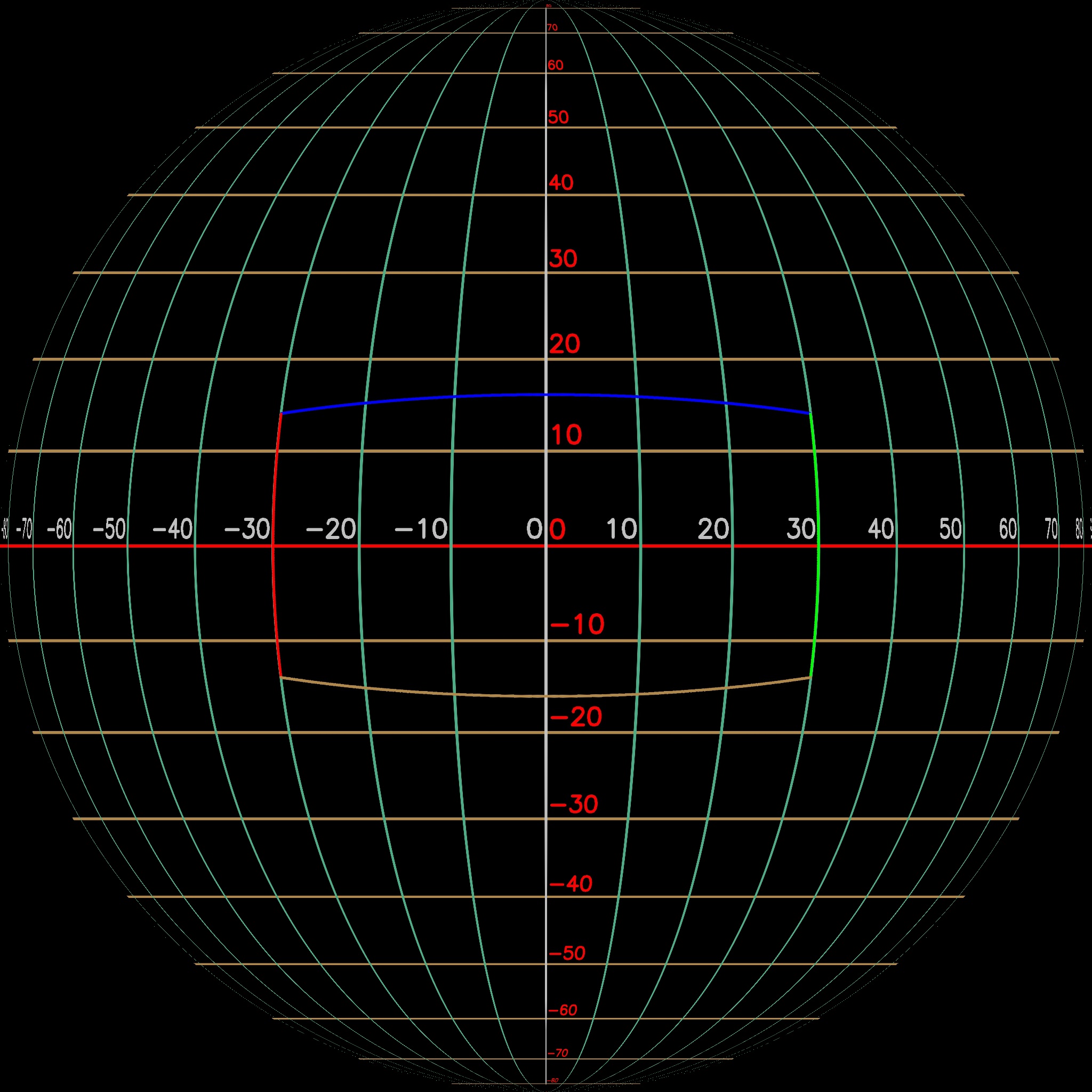
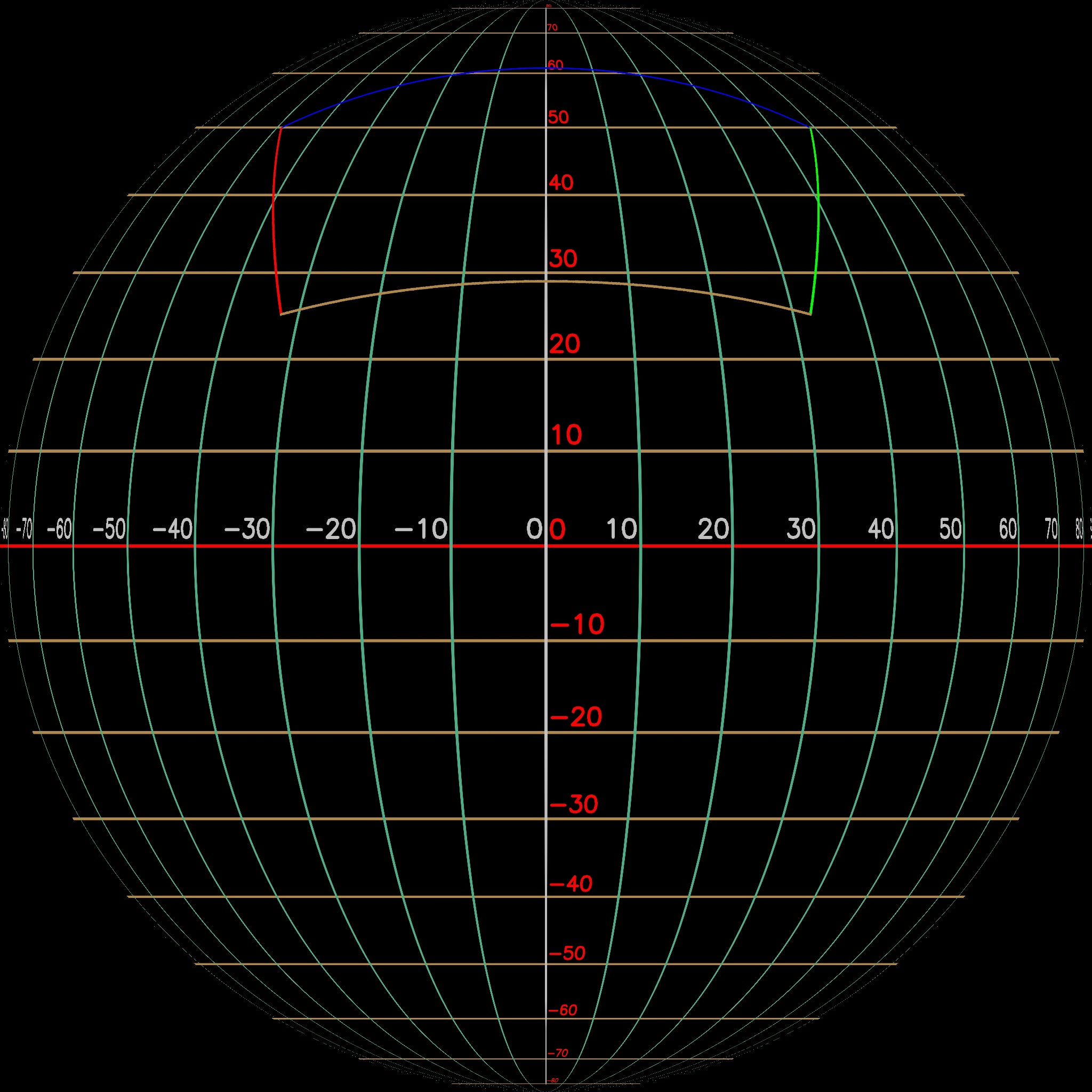
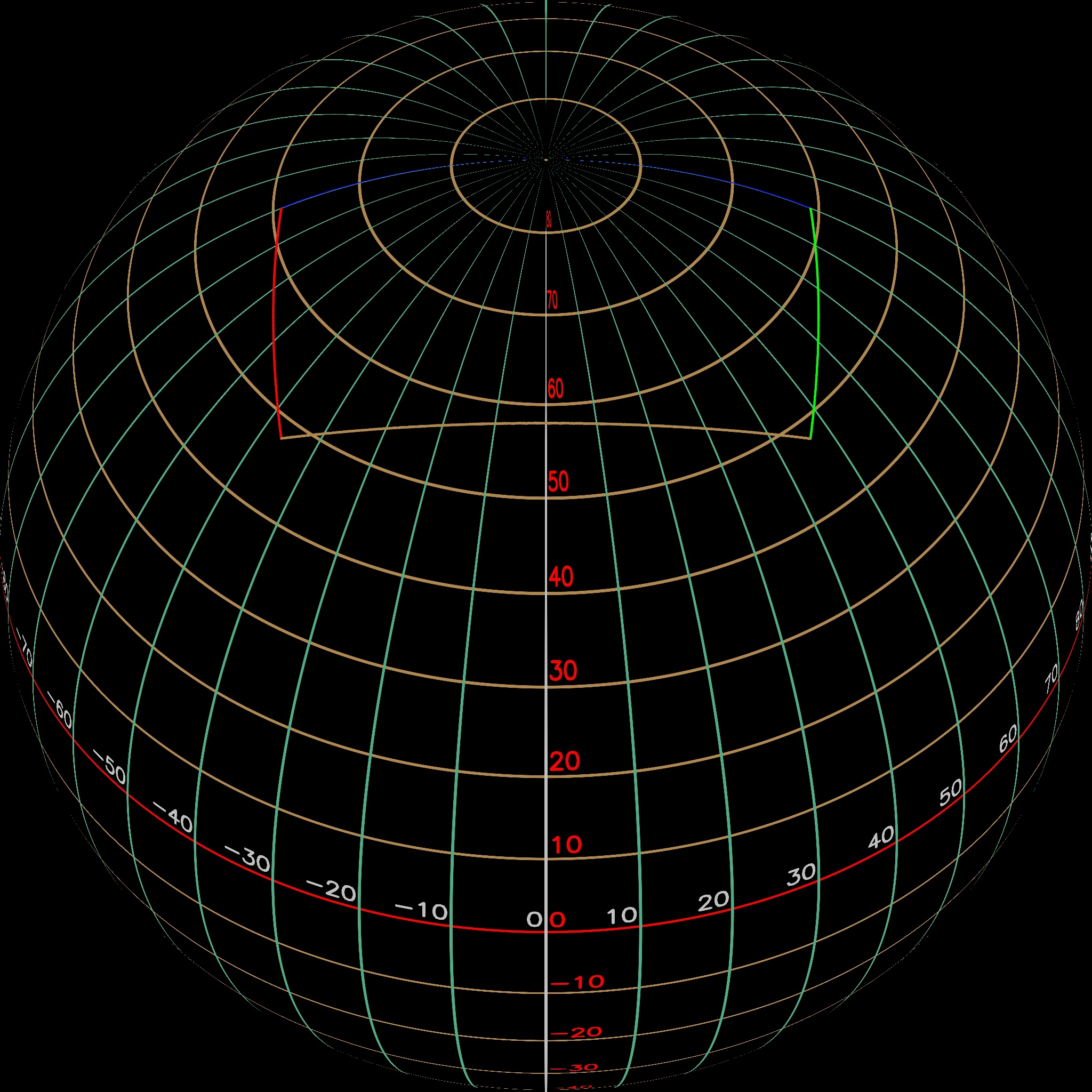
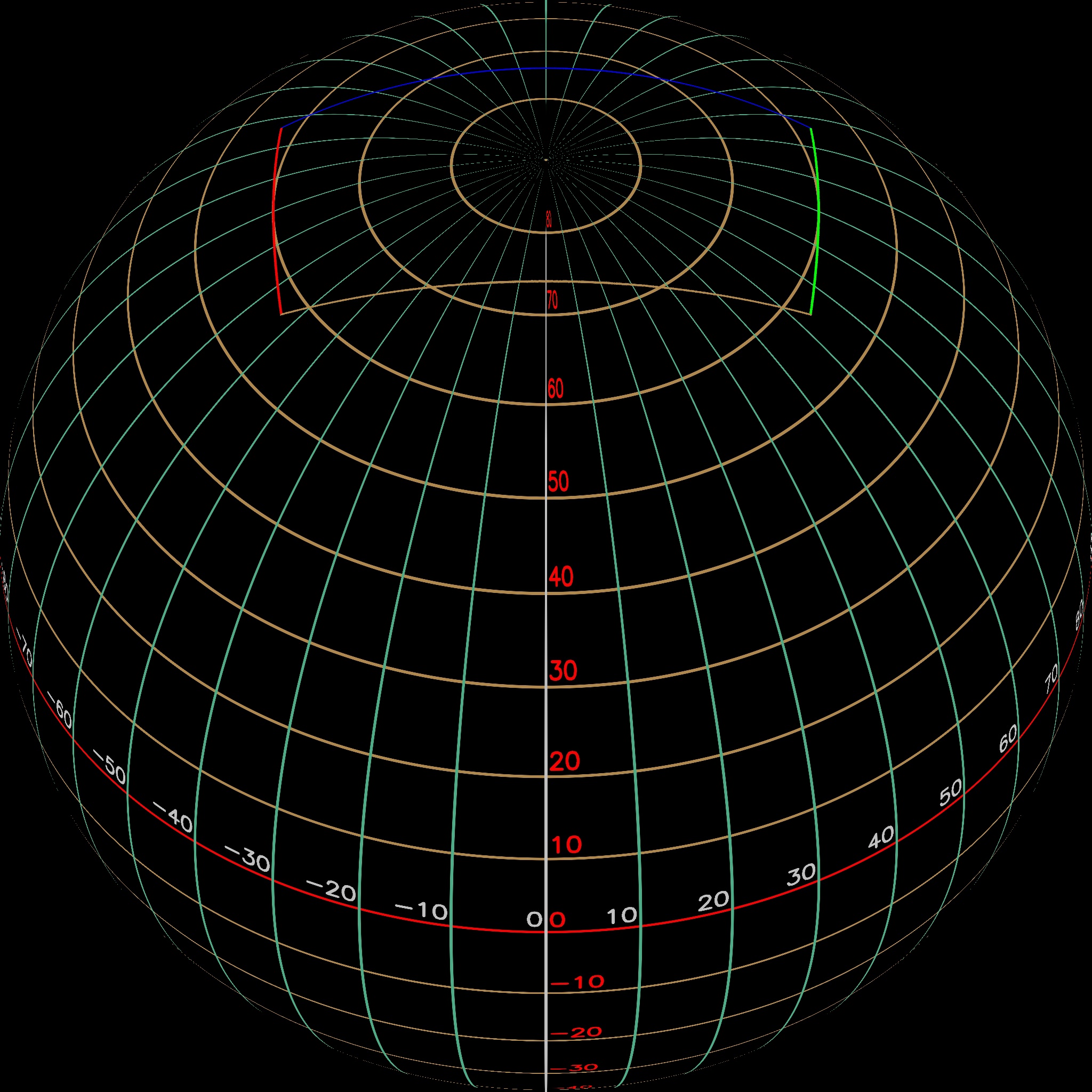
Figures 5, 6, 7, and 8 below set the yaw and roll at 0 degrees, the field of view at 60 degrees, and vary the tilt to 0, 45, 74, and 90 degrees, respectively. The upper left image shows the rectilinear view as viewed from inside the sphere, the lower left image illustrates the bounding box surrounding the image pixels extracted from the equirectangular image, and the right image shows the field of view when projected onto the sphere. The right-hand view was generated from the lower left data using a slightly modified version of code found in the first answer in https://stackoverflow.com/questions/30265375/how-to-draw-orthographic-projection-from-equirectangular-projection. The code was modified since several of the calls used in the original code have been deprecated and removed and only a single frame is created instead of creating the cool gif image shown in the answer.
The field of view "rectangle" outlines the top of the view with a blue line, the right side with green, the bottom with brown, and the left with a red line. This helps us understand the orientation of the rectangle as it is moved around in the equirectangular layout and the spherical layout.


|

|
|
|
Notice how the area of holding the pixels used in the rectilinear image becomes more and more distorted as the field of view moves towards the sphere's north pole.
|
|
As the field of view reaches the sphere's north pole, the top line becomes more and more vertical, and then, as it intersects with the north pole, it splits out to both the right and the left on the equirectangular layout.
|
|
When the field of view looks directly up within the sphere, the rectangle in the equirectangular layout opens up to extract all the pixels around the north pole.
The Cubemap Format captures 360-degree images with a different layout. The efficient layout of the equirectangular format makes it popular; however, the Cubemap format represents the data in a way that is easy for humans to parse if they do not have a viewer. As the format name suggests, the cubemap splits out each side of a cube (Left, Front, Right, Back, Above, and Below) and shows the portion of the image in that direction. Figure 9 shows how the data from Figure 3 appears when saved in one of the cubemap formats.
Conceptually, the faces of the cubemap become folded together to create a cube that surrounds the camera position at the center. The format shown in these figures is not particularly storage efficient given the number of unused pixels (the black regions). However, other cubemap layouts exist where the six faces are stored one after the other either horizontally or vertically. While the storage size is more efficient, visualizing how the cubemap folds into a cube is harder with these layouts.
Alternatively, Figure 10 displays the Cubemap, showing a grid plotted every 10 degrees on each face, and each face is labeled with the direction of the view. For each face, TL = Top Left, TR = Top Right, BL = Bottom Left, and BR = Bottom Right are also shown for orientation.
Using algorithm found in the CubemapConverter class from https://stackoverflow.com/questions/34250742/converting-a-cubemap-into-equirectangular-panorama, a similar Python routine was created that takes each of the 6 faces found in Figure 10 and saves them in equirectangular format, which results in Figure 11. This shows how the mapping algorithm from 360 image coordinates to equirectangular coordinates does interesting things to how the data is captured in the final format and provides some insights into why the image in Figure 2 looks the way it does.
Notice that the lines less than 45 degrees in the Left cubeface appear to break towards the left and then join with the right side as lines greater than 45 degrees. Similarly, lines greater than 45 degrees on the left make a U like shape when joining up to the right side as lines less than 45 degrees. These result from the equirectangular image being wrapped around the sphere.
Figure 13 makes the Cube face representation 50% transparent and overlays it on Figure 2 to assist in understanding how the 360 image coordinates correspond to the equirectangular mapping. Figure 14 allows interacting with the overlay and looking around the scene.
This blog described the two common file representations for 360 image data: 1) equirectangular and 2) cube map. The blog shows examples of both file types and provides various views of the raw data and the extracted field of view to showcase how the formats map the 360-degree data onto a 2D surface.
The next blog in this series (Existing Open Source for 360-Degree Projection) explores existing open-source solutions for extracting a specified view from an equirectangular image and the algorithms being used.

|
Doug Bogia received his Ph.D. in computer science from the University of Illinois, Urbana-Champaign, and works at Intel Corporation. He enjoys photography, woodworking, programming, and optimizing solutions to run as fast as possible on a given piece of hardware. |
© Intel Corporation. Intel, the Intel logo, and other Intel marks are trademarks of Intel Corporation or its subsidiaries. Other names and brands may be claimed as the property of others.